Draw Mohrs Circle Min Stress 4 000 Max Stress 12000

Geometric civil applied science calculation technique

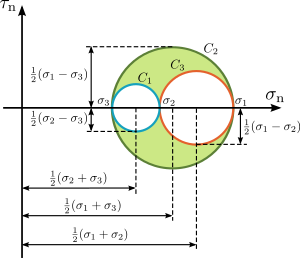
Figure i. Mohr'southward circles for a three-dimensional state of stress

Mohr'southward circle is a ii-dimensional graphical representation of the transformation police for the Cauchy stress tensor.

Mohr's circle is often used in calculations relating to mechanical engineering for materials' force, geotechnical engineering for strength of soils, and structural engineering for strength of built structures. It is also used for computing stresses in many planes by reducing them to vertical and horizontal components. These are called principal planes in which principal stresses are calculated; Mohr's circumvolve can likewise be used to find the principal planes and the principal stresses in a graphical representation, and is one of the easiest means to do so.^[1]

Later on performing a stress analysis on a cloth body causeless as a continuum, the components of the Cauchy stress tensor at a detail material bespeak are known with respect to a coordinate system. The Mohr circle is and so used to determine graphically the stress components acting on a rotated coordinate organization, i.e., acting on a differently oriented aeroplane passing through that signal.

The abscissa and ordinate ( ${\displaystyle \sigma _{\mathrm {n} }}$ , ${\displaystyle \tau _{\mathrm {n} }}$ ) of each bespeak on the circle are the magnitudes of the normal stress and shear stress components, respectively, acting on the rotated coordinate arrangement. In other words, the circle is the locus of points that correspond the state of stress on individual planes at all their orientations, where the axes stand for the principal axes of the stress element.

19th-century German engineer Karl Culmann was the get-go to excogitate a graphical representation for stresses while considering longitudinal and vertical stresses in horizontal beams during bending. His work inspired boyfriend German engineer Christian Otto Mohr (the circle's namesake), who extended it to both two- and iii-dimensional stresses and adult a failure criterion based on the stress circle.^[2]

Culling graphical methods for the representation of the stress country at a indicate include the Lamé'southward stress ellipsoid and Cauchy'due south stress quadric.

The Mohr circle can be applied to any symmetric 2x2 tensor matrix, including the strain and moment of inertia tensors.

Motivation [edit]

Figure 2. Stress in a loaded deformable cloth body causeless every bit a continuum.

Internal forces are produced betwixt the particles of a deformable object, assumed equally a continuum, equally a reaction to applied external forces, i.e., either surface forces or body forces. This reaction follows from Euler's laws of move for a continuum, which are equivalent to Newton'due south laws of motility for a particle. A measure of the intensity of these internal forces is chosen stress. Because the object is assumed equally a continuum, these internal forces are distributed continuously inside the volume of the object.

In engineering science, e.grand., structural, mechanical, or geotechnical, the stress distribution within an object, for instance stresses in a rock mass around a tunnel, airplane wings, or edifice columns, is determined through a stress assay. Calculating the stress distribution implies the determination of stresses at every bespeak (material particle) in the object. According to Cauchy, the stress at any signal in an object (Effigy 2), assumed as a continuum, is completely defined by the 9 stress components ${\displaystyle \sigma _{ij}}$ of a second order tensor of type (2,0) known as the Cauchy stress tensor, ${\displaystyle {\boldsymbol {\sigma }}}$ :

${\displaystyle {\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\\\end{matrix}}\correct]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{y}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{z}\\\end{matrix}}\right]}$

Effigy 3. Stress transformation at a point in a continuum under aeroplane stress atmospheric condition.

Later the stress distribution within the object has been determined with respect to a coordinate system ${\displaystyle (ten,y)}$ , it may exist necessary to summate the components of the stress tensor at a item textile point ${\displaystyle P}$ with respect to a rotated coordinate system ${\displaystyle (ten',y')}$ , i.e., the stresses acting on a airplane with a different orientation passing through that point of interest —forming an angle with the coordinate system ${\displaystyle (x,y)}$ (Figure 3). For case, it is of interest to find the maximum normal stress and maximum shear stress, as well as the orientation of the planes where they act upon. To achieve this, it is necessary to perform a tensor transformation under a rotation of the coordinate arrangement. From the definition of tensor, the Cauchy stress tensor obeys the tensor transformation law. A graphical representation of this transformation law for the Cauchy stress tensor is the Mohr circumvolve for stress.

Mohr's circumvolve for two-dimensional state of stress [edit]

Effigy 4. Stress components at a plane passing through a bespeak in a continuum under plane stress conditions.

In two dimensions, the stress tensor at a given material point ${\displaystyle P}$ with respect to any two perpendicular directions is completely defined past but three stress components. For the detail coordinate organization ${\displaystyle (10,y)}$ these stress components are: the normal stresses ${\displaystyle \sigma _{x}}$ and ${\displaystyle \sigma _{y}}$ , and the shear stress ${\displaystyle \tau _{xy}}$ . From the residuum of angular momentum, the symmetry of the Cauchy stress tensor can be demonstrated. This symmetry implies that ${\displaystyle \tau _{xy}=\tau _{yx}}$ . Thus, the Cauchy stress tensor can be written as:

${\displaystyle {\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{10}&\tau _{xy}&0\\\tau _{xy}&\sigma _{y}&0\\0&0&0\\\terminate{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{10}&\tau _{xy}\\\tau _{xy}&\sigma _{y}\\\end{matrix}}\correct]}$

The objective is to use the Mohr circle to find the stress components ${\displaystyle \sigma _{\mathrm {n} }}$ and ${\displaystyle \tau _{\mathrm {n} }}$ on a rotated coordinate system ${\displaystyle (x',y')}$ , i.e., on a differently oriented plane passing through ${\displaystyle P}$ and perpendicular to the ${\displaystyle x}$ - ${\displaystyle y}$ plane (Figure 4). The rotated coordinate system ${\displaystyle (10',y')}$ makes an angle ${\displaystyle \theta }$ with the original coordinate organisation ${\displaystyle (ten,y)}$ .

Equation of the Mohr circle [edit]

To derive the equation of the Mohr circle for the two-dimensional cases of plane stress and plane strain, outset consider a two-dimensional infinitesimal material element around a material point ${\displaystyle P}$ (Effigy 4), with a unit of measurement area in the management parallel to the ${\displaystyle y}$ - ${\displaystyle z}$ aeroplane, i.eastward., perpendicular to the folio or screen.

From equilibrium of forces on the minute chemical element, the magnitudes of the normal stress ${\displaystyle \sigma _{\mathrm {due north} }}$ and the shear stress ${\displaystyle \tau _{\mathrm {n} }}$ are given by:

${\displaystyle \sigma _{\mathrm {northward} }={\frac {ane}{2}}(\sigma _{10}+\sigma _{y})+{\frac {1}{2}}(\sigma _{10}-\sigma _{y})\cos 2\theta +\tau _{xy}\sin ii\theta }$

${\displaystyle \tau _{\mathrm {northward} }=-{\frac {ane}{ii}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta }$

Derivation of Mohr's circle parametric equations - Equilibrium of forces

From equilibrium of forces in the direction of ${\displaystyle \sigma _{\mathrm {due north} }}$ ( ${\displaystyle 10'}$ -centrality) (Figure 4), and knowing that the surface area of the airplane where ${\displaystyle \sigma _{\mathrm {northward} }}$ acts is ${\displaystyle dA}$ , we have: ${\displaystyle \ {\begin{aligned}\sum F_{x'}&=\sigma _{\mathrm {north} }dA-\sigma _{ten}dA\cos ^{2}\theta -\sigma _{y}dA\sin ^{2}\theta -\tau _{xy}dA\cos \theta \sin \theta -\tau _{xy}dA\sin \theta \cos \theta =0\\\sigma _{\mathrm {northward} }&=\sigma _{x}\cos ^{2}\theta +\sigma _{y}\sin ^{2}\theta +2\tau _{xy}\sin \theta \cos \theta \\\end{aligned}}}$ However, knowing that ${\displaystyle \cos ^{ii}\theta ={\frac {1+\cos ii\theta }{2}},\qquad \sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}\qquad {\text{and}}\qquad \sin 2\theta =2\sin \theta \cos \theta }$ we obtain ${\displaystyle \sigma _{\mathrm {n} }={\frac {i}{two}}(\sigma _{x}+\sigma _{y})+{\frac {i}{2}}(\sigma _{x}-\sigma _{y})\cos ii\theta +\tau _{xy}\sin 2\theta }$ Now, from equilibrium of forces in the direction of ${\displaystyle \tau _{\mathrm {due north} }}$ ( ${\displaystyle y'}$ -centrality) (Figure 4), and knowing that the area of the plane where ${\displaystyle \tau _{\mathrm {n} }}$ acts is ${\displaystyle dA}$ , we have: ${\displaystyle \ {\brainstorm{aligned}\sum F_{y'}&=\tau _{\mathrm {n} }dA+\sigma _{x}dA\cos \theta \sin \theta -\sigma _{y}dA\sin \theta \cos \theta -\tau _{xy}dA\cos ^{two}\theta +\tau _{xy}dA\sin ^{2}\theta =0\\\tau _{\mathrm {due north} }&=-(\sigma _{x}-\sigma _{y})\sin \theta \cos \theta +\tau _{xy}\left(\cos ^{2}\theta -\sin ^{two}\theta \right)\\\stop{aligned}}}$ Withal, knowing that ${\displaystyle \cos ^{2}\theta -\sin ^{two}\theta =\cos 2\theta \qquad {\text{and}}\qquad \sin 2\theta =2\sin \theta \cos \theta }$ we obtain ${\displaystyle \tau _{\mathrm {northward} }=-{\frac {one}{2}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta }$

Both equations can also be obtained by applying the tensor transformation police force on the known Cauchy stress tensor, which is equivalent to performing the static equilibrium of forces in the direction of ${\displaystyle \sigma _{\mathrm {north} }}$ and ${\displaystyle \tau _{\mathrm {due north} }}$ .

Derivation of Mohr'due south circle parametric equations - Tensor transformation

The stress tensor transformation police force tin can be stated as ${\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}'&=\mathbf {A} {\boldsymbol {\sigma }}\mathbf {A} ^{T}\\\left[{\begin{matrix}\sigma _{x'}&\tau _{ten'y'}\\\tau _{y'10'}&\sigma _{y'}\\\cease{matrix}}\right]&=\left[{\brainstorm{matrix}a_{x}&a_{xy}\\a_{yx}&a_{y}\\\end{matrix}}\correct]\left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{yx}&\sigma _{y}\\\end{matrix}}\correct]\left[{\brainstorm{matrix}a_{x}&a_{yx}\\a_{xy}&a_{y}\\\cease{matrix}}\correct]\\&=\left[{\begin{matrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \\\end{matrix}}\right]\left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{yx}&\sigma _{y}\\\end{matrix}}\right]\left[{\begin{matrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{matrix}}\correct]\cease{aligned}}}$ Expanding the right hand side, and knowing that ${\displaystyle \sigma _{x'}=\sigma _{\mathrm {n} }}$ and ${\displaystyle \tau _{ten'y'}=\tau _{\mathrm {due north} }}$ , we have: ${\displaystyle \sigma _{\mathrm {north} }=\sigma _{ten}\cos ^{2}\theta +\sigma _{y}\sin ^{2}\theta +two\tau _{xy}\sin \theta \cos \theta }$ However, knowing that ${\displaystyle \cos ^{ii}\theta ={\frac {1+\cos 2\theta }{2}},\qquad \sin ^{ii}\theta ={\frac {ane-\cos ii\theta }{2}}\qquad {\text{and}}\qquad \sin 2\theta =2\sin \theta \cos \theta }$ nosotros obtain ${\displaystyle \sigma _{\mathrm {northward} }={\frac {1}{2}}(\sigma _{ten}+\sigma _{y})+{\frac {1}{two}}(\sigma _{x}-\sigma _{y})\cos ii\theta +\tau _{xy}\sin ii\theta }$ ${\displaystyle \tau _{\mathrm {north} }=-(\sigma _{x}-\sigma _{y})\sin \theta \cos \theta +\tau _{xy}\left(\cos ^{2}\theta -\sin ^{two}\theta \correct)}$ All the same, knowing that ${\displaystyle \cos ^{2}\theta -\sin ^{2}\theta =\cos ii\theta \qquad {\text{and}}\qquad \sin 2\theta =two\sin \theta \cos \theta }$ we obtain ${\displaystyle \tau _{\mathrm {n} }=-{\frac {1}{ii}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos ii\theta }$ It is not necessary at this moment to calculate the stress component ${\displaystyle \sigma _{y'}}$ acting on the aeroplane perpendicular to the plane of action of ${\displaystyle \sigma _{x'}}$ every bit it is non required for deriving the equation for the Mohr circle.

These two equations are the parametric equations of the Mohr circle. In these equations, ${\displaystyle ii\theta }$ is the parameter, and ${\displaystyle \sigma _{\mathrm {n} }}$ and ${\displaystyle \tau _{\mathrm {n} }}$ are the coordinates. This means that by choosing a coordinate organization with abscissa ${\displaystyle \sigma _{\mathrm {n} }}$ and ordinate ${\displaystyle \tau _{\mathrm {due north} }}$ , giving values to the parameter ${\displaystyle \theta }$ will place the points obtained lying on a circle.

Eliminating the parameter ${\displaystyle 2\theta }$ from these parametric equations will yield the not-parametric equation of the Mohr circle. This can be achieved by rearranging the equations for ${\displaystyle \sigma _{\mathrm {northward} }}$ and ${\displaystyle \tau _{\mathrm {due north} }}$ , first transposing the first term in the commencement equation and squaring both sides of each of the equations and then calculation them. Thus nosotros have

${\displaystyle {\begin{aligned}\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})\right]^{2}+\tau _{\mathrm {n} }^{two}&=\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{ii}+\tau _{xy}^{2}\\(\sigma _{\mathrm {due north} }-\sigma _{\mathrm {avg} })^{2}+\tau _{\mathrm {n} }^{two}&=R^{2}\finish{aligned}}}$

where

${\displaystyle R={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}\quad {\text{and}}\quad \sigma _{\mathrm {avg} }={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})}$

This is the equation of a circumvolve (the Mohr circumvolve) of the form

${\displaystyle (10-a)^{2}+(y-b)^{2}=r^{2}}$

with radius ${\displaystyle r=R}$ centered at a point with coordinates ${\displaystyle (a,b)=(\sigma _{\mathrm {avg} },0)}$ in the ${\displaystyle (\sigma _{\mathrm {due north} },\tau _{\mathrm {n} })}$ coordinate organisation.

Sign conventions [edit]

There are two separate sets of sign conventions that need to be considered when using the Mohr Circumvolve: One sign convention for stress components in the "physical infinite", and another for stress components in the "Mohr-Circle-infinite". In addition, within each of the two set of sign conventions, the engineering mechanics (structural engineering and mechanical engineering) literature follows a different sign convention from the geomechanics literature. In that location is no standard sign convention, and the choice of a particular sign convention is influenced past convenience for adding and interpretation for the particular trouble in hand. A more detailed explanation of these sign conventions is presented below.

The previous derivation for the equation of the Mohr Circle using Figure 4 follows the engineering science mechanics sign convention. The engineering mechanics sign convention will be used for this article.

Physical-space sign convention [edit]

From the convention of the Cauchy stress tensor (Figure three and Figure 4), the showtime subscript in the stress components denotes the face up on which the stress component acts, and the 2d subscript indicates the direction of the stress component. Thus ${\displaystyle \tau _{xy}}$ is the shear stress acting on the face with normal vector in the positive direction of the ${\displaystyle ten}$ -centrality, and in the positive direction of the ${\displaystyle y}$ -axis.

In the physical-space sign convention, positive normal stresses are outward to the plane of activeness (tension), and negative normal stresses are inward to the plane of activeness (compression) (Effigy v).

In the concrete-infinite sign convention, positive shear stresses act on positive faces of the material element in the positive direction of an axis. Also, positive shear stresses human action on negative faces of the material element in the negative direction of an axis. A positive face has its normal vector in the positive management of an axis, and a negative face has its normal vector in the negative direction of an centrality. For example, the shear stresses ${\displaystyle \tau _{xy}}$ and ${\displaystyle \tau _{yx}}$ are positive considering they human activity on positive faces, and they act besides in the positive direction of the ${\displaystyle y}$ -axis and the ${\displaystyle x}$ -axis, respectively (Figure iii). Similarly, the respective reverse shear stresses ${\displaystyle \tau _{xy}}$ and ${\displaystyle \tau _{yx}}$ acting in the negative faces have a negative sign because they act in the negative direction of the ${\displaystyle x}$ -centrality and ${\displaystyle y}$ -axis, respectively.

Mohr-circle-space sign convention [edit]

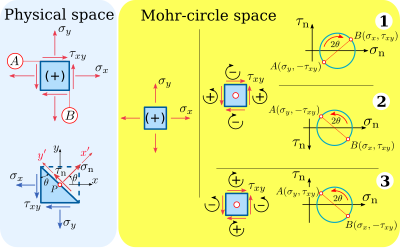
Figure five. Engineering mechanics sign convention for drawing the Mohr circle. This commodity follows sign-convention # iii, as shown.

In the Mohr-circle-infinite sign convention, normal stresses have the same sign as normal stresses in the physical-space sign convention: positive normal stresses deed outward to the aeroplane of activeness, and negative normal stresses act inward to the plane of activeness.

Shear stresses, however, have a different convention in the Mohr-circle space compared to the convention in the physical space. In the Mohr-circumvolve-space sign convention, positive shear stresses rotate the material chemical element in the counterclockwise direction, and negative shear stresses rotate the material in the clockwise management. This style, the shear stress component ${\displaystyle \tau _{xy}}$ is positive in the Mohr-circle space, and the shear stress component ${\displaystyle \tau _{yx}}$ is negative in the Mohr-circle infinite.

Two options exist for drawing the Mohr-circle space, which produce a mathematically correct Mohr circumvolve:

1. Positive shear stresses are plotted upwardly (Figure 5, sign convention #ane)
2. Positive shear stresses are plotted downwardly, i.e., the ${\displaystyle \tau _{\mathrm {n} }}$ -centrality is inverted (Figure five, sign convention #ii).

Plotting positive shear stresses upward makes the angle ${\displaystyle 2\theta }$ on the Mohr circle have a positive rotation clockwise, which is opposite to the concrete space convention. That is why some authors^[3] adopt plotting positive shear stresses downward, which makes the bending ${\displaystyle 2\theta }$ on the Mohr circle have a positive rotation counterclockwise, similar to the physical infinite convention for shear stresses.

To overcome the "event" of having the shear stress centrality downward in the Mohr-circle space, there is an culling sign convention where positive shear stresses are assumed to rotate the textile element in the clockwise direction and negative shear stresses are assumed to rotate the material element in the counterclockwise direction (Effigy 5, option 3). This fashion, positive shear stresses are plotted upwards in the Mohr-circumvolve space and the bending ${\displaystyle ii\theta }$ has a positive rotation counterclockwise in the Mohr-circle infinite. This alternative sign convention produces a circumvolve that is identical to the sign convention #2 in Figure five because a positive shear stress ${\displaystyle \tau _{\mathrm {n} }}$ is too a counterclockwise shear stress, and both are plotted downward. Also, a negative shear stress ${\displaystyle \tau _{\mathrm {n} }}$ is a clockwise shear stress, and both are plotted upward.

This article follows the engineering mechanics sign convention for the physical space and the alternative sign convention for the Mohr-circumvolve space (sign convention #3 in Figure 5)

Drawing Mohr's circle [edit]

Assuming we know the stress components ${\displaystyle \sigma _{x}}$ , ${\displaystyle \sigma _{y}}$ , and ${\displaystyle \tau _{xy}}$ at a point ${\displaystyle P}$ in the object under study, as shown in Figure 4, the post-obit are the steps to construct the Mohr circumvolve for the country of stresses at ${\displaystyle P}$ :

1. Draw the Cartesian coordinate system ${\displaystyle (\sigma _{\mathrm {due north} },\tau _{\mathrm {n} })}$ with a horizontal ${\displaystyle \sigma _{\mathrm {n} }}$ -axis and a vertical ${\displaystyle \tau _{\mathrm {n} }}$ -centrality.
2. Plot 2 points ${\displaystyle A(\sigma _{y},\tau _{xy})}$ and ${\displaystyle B(\sigma _{x},-\tau _{xy})}$ in the ${\displaystyle (\sigma _{\mathrm {due north} },\tau _{\mathrm {n} })}$ space corresponding to the known stress components on both perpendicular planes ${\displaystyle A}$ and ${\displaystyle B}$ , respectively (Figure 4 and half-dozen), following the chosen sign convention.
3. Depict the bore of the circumvolve by joining points ${\displaystyle A}$ and ${\displaystyle B}$ with a straight line ${\displaystyle {\overline {AB}}}$ .
4. Draw the Mohr Circle. The centre ${\displaystyle O}$ of the circle is the midpoint of the diameter line ${\displaystyle {\overline {AB}}}$ , which corresponds to the intersection of this line with the ${\displaystyle \sigma _{\mathrm {n} }}$ axis.

Finding principal normal stresses [edit]

Stress components on a 2D rotating element. Example of how stress components vary on the faces (edges) of a rectangular element equally the angle of its orientation is varied. Principal stresses occur when the shear stresses simultaneously disappear from all faces. The orientation at which this occurs gives the principal directions. In this example, when the rectangle is horizontal, the stresses are given by ${\displaystyle \left[{\brainstorm{matrix}\sigma _{xx}&\tau _{xy}\\\tau _{yx}&\sigma _{yy}\end{matrix}}\right]=\left[{\begin{matrix}-10&10\\10&fifteen\end{matrix}}\right].}$ The respective Mohr's circle representation is shown at the bottom.

The magnitude of the principal stresses are the abscissas of the points ${\displaystyle C}$ and ${\displaystyle E}$ (Figure 6) where the circle intersects the ${\displaystyle \sigma _{\mathrm {n} }}$ -axis. The magnitude of the major chief stress ${\displaystyle \sigma _{one}}$ is always the greatest absolute value of the abscissa of any of these 2 points. Likewise, the magnitude of the pocket-sized principal stress ${\displaystyle \sigma _{two}}$ is always the everyman absolute value of the abscissa of these two points. As expected, the ordinates of these ii points are zip, corresponding to the magnitude of the shear stress components on the principal planes. Alternatively, the values of the principal stresses can exist found by

${\displaystyle \sigma _{1}=\sigma _{\max }=\sigma _{\text{avg}}+R}$

${\displaystyle \sigma _{2}=\sigma _{\min }=\sigma _{\text{avg}}-R}$

where the magnitude of the boilerplate normal stress ${\displaystyle \sigma _{\text{avg}}}$ is the abscissa of the centre ${\displaystyle O}$ , given by

${\displaystyle \sigma _{\text{avg}}={\tfrac {1}{2}}(\sigma _{ten}+\sigma _{y})}$

and the length of the radius ${\displaystyle R}$ of the circumvolve (based on the equation of a circle passing through 2 points), is given by

${\displaystyle R={\sqrt {\left[{\tfrac {1}{ii}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}}$

Finding maximum and minimum shear stresses [edit]

The maximum and minimum shear stresses correspond to the ordinates of the highest and lowest points on the circle, respectively. These points are located at the intersection of the circle with the vertical line passing through the centre of the circle, ${\displaystyle O}$ . Thus, the magnitude of the maximum and minimum shear stresses are equal to the value of the circle's radius ${\displaystyle R}$

${\displaystyle \tau _{\max ,\min }=\pm R}$

Finding stress components on an capricious plane [edit]

Equally mentioned before, after the two-dimensional stress analysis has been performed we know the stress components ${\displaystyle \sigma _{x}}$ , ${\displaystyle \sigma _{y}}$ , and ${\displaystyle \tau _{xy}}$ at a cloth betoken ${\displaystyle P}$ . These stress components human action in two perpendicular planes ${\displaystyle A}$ and ${\displaystyle B}$ passing through ${\displaystyle P}$ as shown in Figure 5 and 6. The Mohr circle is used to find the stress components ${\displaystyle \sigma _{\mathrm {n} }}$ and ${\displaystyle \tau _{\mathrm {n} }}$ , i.e., coordinates of any point ${\displaystyle D}$ on the circle, acting on any other airplane ${\displaystyle D}$ passing through ${\displaystyle P}$ making an bending ${\displaystyle \theta }$ with the aeroplane ${\displaystyle B}$ . For this, two approaches can exist used: the double bending, and the Pole or origin of planes.

Double bending [edit]

As shown in Figure half dozen, to determine the stress components ${\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {north} })}$ acting on a plane ${\displaystyle D}$ at an angle ${\displaystyle \theta }$ counterclockwise to the plane ${\displaystyle B}$ on which ${\displaystyle \sigma _{10}}$ acts, we travel an angle ${\displaystyle 2\theta }$ in the aforementioned counterclockwise direction effectually the circle from the known stress point ${\displaystyle B(\sigma _{x},-\tau _{xy})}$ to betoken ${\displaystyle D(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}$ , i.east., an angle ${\displaystyle two\theta }$ between lines ${\displaystyle {\overline {OB}}}$ and ${\displaystyle {\overline {OD}}}$ in the Mohr circle.

The double bending arroyo relies on the fact that the bending ${\displaystyle \theta }$ between the normal vectors to any ii concrete planes passing through ${\displaystyle P}$ (Effigy 4) is one-half the bending between two lines joining their corresponding stress points ${\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}$ on the Mohr circle and the center of the circle.

This double angle relation comes from the fact that the parametric equations for the Mohr circumvolve are a function of ${\displaystyle ii\theta }$ . It can also be seen that the planes ${\displaystyle A}$ and ${\displaystyle B}$ in the cloth element effectually ${\displaystyle P}$ of Figure 5 are separated by an angle ${\displaystyle \theta =ninety^{\circ }}$ , which in the Mohr circle is represented by a ${\displaystyle 180^{\circ }}$ angle (double the angle).

Pole or origin of planes [edit]

Figure 7. Mohr's circle for airplane stress and plane strain conditions (Pole approach). Any straight line drawn from the pole volition intersect the Mohr circle at a point that represents the state of stress on a plane inclined at the same orientation (parallel) in infinite every bit that line.

The 2nd arroyo involves the determination of a point on the Mohr circumvolve chosen the pole or the origin of planes. Any straight line drawn from the pole will intersect the Mohr circumvolve at a signal that represents the state of stress on a airplane inclined at the same orientation (parallel) in infinite as that line. Therefore, knowing the stress components ${\displaystyle \sigma }$ and ${\displaystyle \tau }$ on whatsoever item airplane, one can draw a line parallel to that plane through the detail coordinates ${\displaystyle \sigma _{\mathrm {n} }}$ and ${\displaystyle \tau _{\mathrm {n} }}$ on the Mohr circle and find the pole as the intersection of such line with the Mohr circle. As an example, permit's assume we have a state of stress with stress components ${\displaystyle \sigma _{x},\!}$ , ${\displaystyle \sigma _{y},\!}$ , and ${\displaystyle \tau _{xy},\!}$ , as shown on Effigy seven. Showtime, we can depict a line from point ${\displaystyle B}$ parallel to the plane of action of ${\displaystyle \sigma _{10}}$ , or, if nosotros choose otherwise, a line from indicate ${\displaystyle A}$ parallel to the airplane of action of ${\displaystyle \sigma _{y}}$ . The intersection of whatever of these two lines with the Mohr circumvolve is the pole. One time the pole has been determined, to find the state of stress on a aeroplane making an bending ${\displaystyle \theta }$ with the vertical, or in other words a plane having its normal vector forming an angle ${\displaystyle \theta }$ with the horizontal plane, and then we can draw a line from the pole parallel to that plane (Run into Figure 7). The normal and shear stresses on that airplane are then the coordinates of the point of intersection between the line and the Mohr circle.

Finding the orientation of the principal planes [edit]

The orientation of the planes where the maximum and minimum principal stresses deed, also known equally principal planes, can be determined by measuring in the Mohr circle the angles ∠BOC and ∠BOE, respectively, and taking half of each of those angles. Thus, the angle ∠BOC between ${\displaystyle {\overline {OB}}}$ and ${\displaystyle {\overline {OC}}}$ is double the bending ${\displaystyle \theta _{p}}$ which the major principal plane makes with plane ${\displaystyle B}$ .

Angles ${\displaystyle \theta _{p1}}$ and ${\displaystyle \theta _{p2}}$ tin also be found from the post-obit equation

${\displaystyle \tan 2\theta _{\mathrm {p} }={\frac {2\tau _{xy}}{\sigma _{y}-\sigma _{ten}}}}$

This equation defines ii values for ${\displaystyle \theta _{\mathrm {p} }}$ which are ${\displaystyle 90^{\circ }}$ apart (Effigy). This equation can be derived direct from the geometry of the circle, or by making the parametric equation of the circle for ${\displaystyle \tau _{\mathrm {northward} }}$ equal to zip (the shear stress in the principal planes is always zero).

Example [edit]

Assume a material element under a state of stress as shown in Figure 8 and Figure 9, with the plane of one of its sides oriented x° with respect to the horizontal plane. Using the Mohr circle, discover:

• The orientation of their planes of action.
• The maximum shear stresses and orientation of their planes of action.
• The stress components on a horizontal aeroplane.

Check the answers using the stress transformation formulas or the stress transformation law.

Solution: Following the engineering science mechanics sign convention for the concrete space (Effigy 5), the stress components for the material chemical element in this example are:

${\displaystyle \sigma _{x'}=-10{\textrm {MPa}}}$

${\displaystyle \sigma _{y'}=50{\textrm {MPa}}}$

${\displaystyle \tau _{10'y'}=40{\textrm {MPa}}}$ .

Following the steps for drawing the Mohr circle for this item state of stress, we first describe a Cartesian coordinate arrangement ${\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {northward} })}$ with the ${\displaystyle \tau _{\mathrm {n} }}$ -axis upward.

We then plot 2 points A(50,40) and B(-x,-xl), representing the state of stress at airplane A and B every bit show in both Figure viii and Figure 9. These points follow the engineering mechanics sign convention for the Mohr-circle infinite (Effigy five), which assumes positive normals stresses outward from the fabric element, and positive shear stresses on each plane rotating the material chemical element clockwise. This way, the shear stress interim on aeroplane B is negative and the shear stress interim on aeroplane A is positive. The diameter of the circumvolve is the line joining point A and B. The eye of the circle is the intersection of this line with the ${\displaystyle \sigma _{\mathrm {n} }}$ -centrality. Knowing both the location of the centre and length of the bore, nosotros are able to plot the Mohr circumvolve for this particular state of stress.

The abscissas of both points E and C (Effigy eight and Effigy 9) intersecting the ${\displaystyle \sigma _{\mathrm {n} }}$ -axis are the magnitudes of the minimum and maximum normal stresses, respectively; the ordinates of both points E and C are the magnitudes of the shear stresses acting on both the minor and major principal planes, respectively, which is zero for chief planes.

Fifty-fifty though the idea for using the Mohr circumvolve is to graphically discover different stress components by actually measuring the coordinates for dissimilar points on the circle, it is more convenient to ostend the results analytically. Thus, the radius and the abscissa of the centre of the circle are

${\displaystyle {\brainstorm{aligned}R&={\sqrt {\left[{\tfrac {i}{two}}(\sigma _{ten}-\sigma _{y})\correct]^{two}+\tau _{xy}^{2}}}\\&={\sqrt {\left[{\tfrac {ane}{two}}(-x-l)\right]^{2}+40^{2}}}\\&=50{\textrm {MPa}}\\\cease{aligned}}}$

${\displaystyle {\begin{aligned}\sigma _{\mathrm {avg} }&={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})\\&={\tfrac {1}{2}}(-10+l)\\&=20{\textrm {MPa}}\\\end{aligned}}}$

and the main stresses are

${\displaystyle {\begin{aligned}\sigma _{1}&=\sigma _{\mathrm {avg} }+R\\&=70{\textrm {MPa}}\\\stop{aligned}}}$

${\displaystyle {\brainstorm{aligned}\sigma _{2}&=\sigma _{\mathrm {avg} }-R\\&=-30{\textrm {MPa}}\\\terminate{aligned}}}$

The coordinates for both points H and One thousand (Figure 8 and Figure 9) are the magnitudes of the minimum and maximum shear stresses, respectively; the abscissas for both points H and G are the magnitudes for the normal stresses interim on the same planes where the minimum and maximum shear stresses human action, respectively. The magnitudes of the minimum and maximum shear stresses tin can be found analytically by

${\displaystyle \tau _{\max ,\min }=\pm R=\pm 50{\textrm {MPa}}}$

and the normal stresses acting on the same planes where the minimum and maximum shear stresses act are equal to ${\displaystyle \sigma _{\mathrm {avg} }}$

We can choose to either use the double bending approach (Figure viii) or the Pole approach (Figure 9) to find the orientation of the main normal stresses and master shear stresses.

Using the double angle approach we measure out the angles ∠BOC and ∠BOE in the Mohr Circumvolve (Figure 8) to find double the angle the major principal stress and the minor primary stress make with airplane B in the concrete space. To obtain a more than accurate value for these angles, instead of manually measuring the angles, we can use the belittling expression

${\displaystyle {\begin{aligned}2\theta _{\mathrm {p} }=\arctan {\frac {2\tau _{xy}}{\sigma _{x}-\sigma _{y}}}=\arctan {\frac {2*40}{(-10-50)}}=-\arctan {\frac {four}{3}}\end{aligned}}}$

One solution is: ${\displaystyle 2\theta _{p}=-53.thirteen^{\circ }}$ . From inspection of Effigy eight, this value corresponds to the bending ∠BOE. Thus, the minor principal angle is

${\displaystyle \theta _{p2}=-26.565^{\circ }}$

And so, the major master angle is

${\displaystyle {\brainstorm{aligned}2\theta _{p1}&=180-53.13^{\circ }=126.87^{\circ }\\\theta _{p1}&=63.435^{\circ }\\\cease{aligned}}}$

Remember that in this detail case ${\displaystyle \theta _{p1}}$ and ${\displaystyle \theta _{p2}}$ are angles with respect to the plane of action of ${\displaystyle \sigma _{ten'}}$ (oriented in the ${\displaystyle x'}$ -centrality)and non angles with respect to the plane of action of ${\displaystyle \sigma _{x}}$ (oriented in the ${\displaystyle 10}$ -axis).

Using the Pole approach, we first localize the Pole or origin of planes. For this, we draw through point A on the Mohr circle a line inclined ten° with the horizontal, or, in other words, a line parallel to airplane A where ${\displaystyle \sigma _{y'}}$ acts. The Pole is where this line intersects the Mohr circle (Figure 9). To confirm the location of the Pole, we could draw a line through point B on the Mohr circle parallel to the plane B where ${\displaystyle \sigma _{10'}}$ acts. This line would also intersect the Mohr circumvolve at the Pole (Figure ix).

From the Pole, nosotros draw lines to dissimilar points on the Mohr circumvolve. The coordinates of the points where these lines intersect the Mohr circle signal the stress components interim on a plane in the physical space having the aforementioned inclination as the line. For instance, the line from the Pole to point C in the circle has the same inclination as the plane in the physical infinite where ${\displaystyle \sigma _{ane}}$ acts. This aeroplane makes an angle of 63.435° with plane B, both in the Mohr-circle infinite and in the concrete space. In the same mode, lines are traced from the Pole to points E, D, F, G and H to detect the stress components on planes with the same orientation.

Mohr's circle for a general three-dimensional state of stresses [edit]

Figure 10. Mohr'due south circle for a 3-dimensional state of stress

To construct the Mohr circle for a full general three-dimensional case of stresses at a indicate, the values of the master stresses ${\displaystyle \left(\sigma _{one},\sigma _{2},\sigma _{3}\correct)}$ and their principal directions ${\displaystyle \left(n_{i},n_{2},n_{3}\correct)}$ must exist commencement evaluated.

Because the main axes as the coordinate arrangement, instead of the general ${\displaystyle x_{1}}$ , ${\displaystyle x_{2}}$ , ${\displaystyle x_{3}}$ coordinate system, and assuming that ${\displaystyle \sigma _{ane}>\sigma _{ii}>\sigma _{iii}}$ , and so the normal and shear components of the stress vector ${\displaystyle \mathbf {T} ^{(\mathbf {northward} )}}$ , for a given plane with unit vector ${\displaystyle \mathbf {north} }$ , satisfy the following equations

${\displaystyle {\begin{aligned}\left(T^{(due north)}\right)^{2}&=\sigma _{ij}\sigma _{ik}n_{j}n_{1000}\\\sigma _{\mathrm {n} }^{2}+\tau _{\mathrm {due north} }^{ii}&=\sigma _{ane}^{2}n_{one}^{2}+\sigma _{2}^{2}n_{2}^{2}+\sigma _{3}^{2}n_{iii}^{ii}\end{aligned}}}$

${\displaystyle \sigma _{\mathrm {n} }=\sigma _{ane}n_{i}^{2}+\sigma _{ii}n_{2}^{2}+\sigma _{iii}n_{3}^{2}.}$

Knowing that ${\displaystyle n_{i}n_{i}=n_{1}^{ii}+n_{2}^{2}+n_{3}^{2}=1}$ , we can solve for ${\displaystyle n_{1}^{2}}$ , ${\displaystyle n_{2}^{2}}$ , ${\displaystyle n_{3}^{2}}$ , using the Gauss elimination method which yields

${\displaystyle {\begin{aligned}n_{1}^{2}&={\frac {\tau _{\mathrm {due north} }^{2}+(\sigma _{\mathrm {northward} }-\sigma _{two})(\sigma _{\mathrm {n} }-\sigma _{3})}{(\sigma _{ane}-\sigma _{2})(\sigma _{1}-\sigma _{3})}}\geq 0\\n_{ii}^{2}&={\frac {\tau _{\mathrm {n} }^{two}+(\sigma _{\mathrm {north} }-\sigma _{three})(\sigma _{\mathrm {n} }-\sigma _{1})}{(\sigma _{2}-\sigma _{3})(\sigma _{2}-\sigma _{1})}}\geq 0\\n_{3}^{2}&={\frac {\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{1})(\sigma _{\mathrm {n} }-\sigma _{ii})}{(\sigma _{three}-\sigma _{1})(\sigma _{iii}-\sigma _{two})}}\geq 0.\end{aligned}}}$

Since ${\displaystyle \sigma _{1}>\sigma _{two}>\sigma _{3}}$ , and ${\displaystyle (n_{i})^{2}}$ is non-negative, the numerators from these equations satisfy

${\displaystyle \tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{2})(\sigma _{\mathrm {northward} }-\sigma _{3})\geq 0}$ as the denominator ${\displaystyle \sigma _{one}-\sigma _{2}>0}$ and ${\displaystyle \sigma _{1}-\sigma _{3}>0}$

${\displaystyle \tau _{\mathrm {n} }^{two}+(\sigma _{\mathrm {northward} }-\sigma _{3})(\sigma _{\mathrm {n} }-\sigma _{1})\leq 0}$ as the denominator ${\displaystyle \sigma _{ii}-\sigma _{3}>0}$ and ${\displaystyle \sigma _{2}-\sigma _{one}<0}$

${\displaystyle \tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{ane})(\sigma _{\mathrm {n} }-\sigma _{2})\geq 0}$ as the denominator ${\displaystyle \sigma _{three}-\sigma _{1}<0}$ and ${\displaystyle \sigma _{three}-\sigma _{2}<0.}$

These expressions can be rewritten equally

${\displaystyle {\begin{aligned}\tau _{\mathrm {n} }^{ii}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{2}+\sigma _{iii})\right]^{ii}\geq \left({\tfrac {1}{2}}(\sigma _{two}-\sigma _{3})\right)^{2}\\\tau _{\mathrm {north} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{i}+\sigma _{iii})\right]^{2}\leq \left({\tfrac {1}{two}}(\sigma _{1}-\sigma _{three})\right)^{2}\\\tau _{\mathrm {due north} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{i}+\sigma _{ii})\right]^{2}\geq \left({\tfrac {1}{2}}(\sigma _{1}-\sigma _{2})\right)^{2}\\\terminate{aligned}}}$

which are the equations of the three Mohr'southward circles for stress ${\displaystyle C_{1}}$ , ${\displaystyle C_{2}}$ , and ${\displaystyle C_{3}}$ , with radii ${\displaystyle R_{1}={\tfrac {1}{2}}(\sigma _{2}-\sigma _{3})}$ , ${\displaystyle R_{2}={\tfrac {1}{2}}(\sigma _{1}-\sigma _{3})}$ , and ${\displaystyle R_{3}={\tfrac {1}{2}}(\sigma _{i}-\sigma _{ii})}$ , and their centres with coordinates ${\displaystyle \left[{\tfrac {1}{2}}(\sigma _{two}+\sigma _{3}),0\correct]}$ , ${\displaystyle \left[{\tfrac {1}{2}}(\sigma _{1}+\sigma _{3}),0\right]}$ , ${\displaystyle \left[{\tfrac {ane}{2}}(\sigma _{one}+\sigma _{2}),0\right]}$ , respectively.

These equations for the Mohr circles show that all admissible stress points ${\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {northward} })}$ lie on these circles or within the shaded area enclosed by them (run into Figure 10). Stress points ${\displaystyle (\sigma _{\mathrm {north} },\tau _{\mathrm {north} })}$ satisfying the equation for circumvolve ${\displaystyle C_{1}}$ lie on, or outside circle ${\displaystyle C_{i}}$ . Stress points ${\displaystyle (\sigma _{\mathrm {due north} },\tau _{\mathrm {n} })}$ satisfying the equation for circle ${\displaystyle C_{2}}$ lie on, or inside circumvolve ${\displaystyle C_{2}}$ . And finally, stress points ${\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}$ satisfying the equation for circle ${\displaystyle C_{3}}$ lie on, or outside circle ${\displaystyle C_{3}}$ .

See also [edit]

• Critical plane analysis

References [edit]

1. ^ "Principal stress and principal aeroplane". world wide web.engineeringapps.net . Retrieved 2019-12-25 .
2. ^ Parry, Richard Hawley Greyness (2004). Mohr circles, stress paths and geotechnics (2 ed.). Taylor & Francis. pp. 1–30. ISBN0-415-27297-1.
3. ^ Gere, James M. (2013). Mechanics of Materials. Goodno, Barry J. (8th ed.). Stamford, CT: Cengage Learning. ISBN9781111577735.

Bibliography [edit]

• Beer, Ferdinand Pierre; Elwood Russell Johnston; John T. DeWolf (1992). Mechanics of Materials . McGraw-Hill Professional person. ISBN0-07-112939-1.
• Brady, B.H.Thousand.; E.T. Brown (1993). Rock Mechanics For Underground Mining (3rd ed.). Kluwer Academic Publisher. pp. 17–29. ISBN0-412-47550-2.
• Davis, R. O.; Selvadurai. A. P. S. (1996). Elasticity and geomechanics. Cambridge University Press. pp. 16–26. ISBN0-521-49827-9.
• Holtz, Robert D.; Kovacs, William D. (1981). An introduction to geotechnical applied science. Prentice-Hall civil engineering and engineering mechanics series. Prentice-Hall. ISBN0-13-484394-0.
• Jaeger, John Conrad; Cook, Due north.Thousand.Due west.; Zimmerman, R.W. (2007). Fundamentals of rock mechanics (Fourth ed.). Wiley-Blackwell. pp. 9–41. ISBN978-0-632-05759-7.
• Jumikis, Alfreds R. (1969). Theoretical soil mechanics: with practical applications to soil mechanics and foundation engineering. Van Nostrand Reinhold Co. ISBN0-442-04199-3.
• Parry, Richard Hawley Grey (2004). Mohr circles, stress paths and geotechnics (ii ed.). Taylor & Francis. pp. 1–30. ISBN0-415-27297-i.
• Timoshenko, Stephen P.; James Norman Goodier (1970). Theory of Elasticity (Tertiary ed.). McGraw-Hill International Editions. ISBN0-07-085805-5.
• Timoshenko, Stephen P. (1983). History of force of materials: with a brief business relationship of the history of theory of elasticity and theory of structures. Dover Books on Physics. Dover Publications. ISBN0-486-61187-half dozen.

External links [edit]

• Mohr'southward Circumvolve and more circles by Rebecca Brannon
• DoITPoMS Teaching and Learning Package- "Stress Analysis and Mohr's Circumvolve"

bellfarly1953.blogspot.com

Source: https://en.wikipedia.org/wiki/Mohr%27s_circle

Share this post